• TOUS LES FRUITS
• POMME - APPLE
• POIRE - PEAR
• PRUNUS
  • ABRICOTS - APRICOT
  • AMANDE - ALMOND
  • CERISE - CHERRY
  • PECHE - PEACH
  • PRUNE - PLUM
• FRAISE - STRAWBERRY
• GROSEILLE - CURRANT
• RUBUS
  • FRAMBOISE - RASPBERRY
  • MURE - BLACKBERRY
• RAISIN - GRAPE
• COING - QUINCE
• FRUITS A COQUE - SKIFF FRUITS
  • NOISETTE - HAZELNUT
  • NOIX - WALNUT
  • LA CHATAIGNE - THE CHESTNUT
• FRUITS DIVERS - MIscellaneous
• FRUITS SAUVAGES - WILD FRUITS
• TOMATE - TOMATO

 

Arboriculture et Mathématiques :
La modélisation des phénomènes
d'auto-organisation

Mais à quoi les chercheurs en mathématiques réfléchissent-ils donc dans leur laboratoire? Cette question, nous sommes nombreux à nous l'être déjà posée! En fait, les mathématiques appliquées servent à mieux comprendre le monde qui nous entoure en essayant de bâtir un modèle du phénomène que l'on étudie. Le modèle mathématique de ce phénomène peut ensuite, lorsqu'il est établi et vérifié par l'expérience, être utilisé pour en prévoir son évolution. Très concrètement, prenons l'exemple de la croissance d'un arbre fruitier. En s'appuyant sur des observations en verger qui permettent de définir les modèles de ramification pour une espèce ou une variété donnée, on peut établir un algorithme mathématique de croissance et on pourra ainsi prévoir la forme probable d'un arbre à l'âge adulte. Pour illustrer ce propos, voyez sous  http://raphaello.univ-fcomte.fr/These/Chapitre3.htm

les différentes images d'arbres synthétisées par ordinateur : leur réalisme est saisissant. Une fois le phénomène décrit par des équations de base, on peut les rendre plus complexe pour faire tenir compte au modèle de tout un tas de paramètres. Revenons à notre arbre fruitier : lorsque le modèle mathématique calcule la croissance de l'arbre, on peut lui demander, en définissant des critères adaptés, de supprimer un certain nombre de branches. La forme calculée de l'arbre intégrera alors l'influence de la taille réalisée... La puissance, mais aussi la beauté, de la modélisation est qu'elle peut étendre l'expérience à un nombre infini de cas, et faire gagner beaucoup de temps dans la compréhension d'un phénomène. En arboriculture fruitière, de nombreuses données peuvent être déduites de ces calculs : le nombre de feuilles, la surface foliaire, le rapport feuilles/fruits. Si on modélise l'ensoleillement d'une région, on peut par simulation estimer l'intensité de la photosynthèse à n'importe quel endroit dans la ramure de l'arbre, et donc prévoir la qualité et la quantité de fruits récoltés en fonction de leur positionnement dans l'arbre. Sous http://raphaello.univ-fcomte.fr/These/Chapitre7.htm , paragraphe 7.3.7, vous verrez comment on peut calculer les ombres portées dans la ramure sur un modèle virtuel d'arbre.

Le but ultime de la modélisation serait alors d'étudier les différents systèmes de conduite ( Axe vertical, Fuseau, Solaxe, V-Güttingen, Ycare,

Mikado, Drilling,…) avec différents principes de taille (taille longue, conduite centrifuge, extinction artificielle,…) sans plus avoir à planter les arbres, faire les essais en plein champ et attendre des années que tout cela pousse. Le verger idéal avec la méthode de conduite et la technique de taille adaptée serait simulé par ordinateur avant d'être planté… Actuellement, quelques laboratoires de recherche en arboriculture fruitière travaillent sur la digitalisation et la modélisation 3D des arbres fruitiers (INRA et CIRAD en France, RAC en Suisse : 2 publications de Ph. Monney peuvent être téléchargées  sous http://www.racchangins.ch/doc/fr/chercheurs/arbor/mode_conduite.html).

Mais sur quelles théories se basent ces modèles? Et bien, ces théories sont si nombreuses et si complexes qu'il serait impossible d'en donner ici ne serait-ce qu'une description succincte! Les nombres fractals, les théories du chaos, les théories des L-Systèmes, les théories des phénomènes d'auto-organisation sont autant de modèles élaborés par les mathématiciens pour comprendre, décrire et modéliser les phénomènes naturels, qu'ils soient d'ailleurs du monde vivant ou du monde minéral. Pour en savoir plus sur les fractals, lisez ce très bel article sous http://www.up.univ-mrs.fr/~ufrsm/filieres/LicPlurid/fractales/fractaleweb.html .

Aussi, pour bien saisir comment les mathématiques et la compréhension de la nature sont liées, nous allons nous pencher sur une toute petite partie de cet immense champ de recherches en abordant quelques exemples d'auto-organisation dans la nature : les phénomènes de ramification, qui permettent de modéliser la croissance d'un arbre, sont des exemples typiques d'auto-organisation. Pour cela, revenons à quelques bases simples.
On sait que TOUT, la matière vivante comme la matière minérale, obéit à des lois physiques fondamentales. Ainsi, de la structuration de la double hélice d'ADN à la formation des galaxies en passant par l’organisation des tissus biologiques ou la ramification d’un arbre, tout obéit à des lois comme la pesanteur ou le frottement. Même si dans la nature la diversité des formes est infinie, on a constaté récemment que très peu de lois physiques peuvent produire cette très grande diversité. Selon la taille des objets, de l'infiniment petit à l'infiniment grand, et la nature des matériaux qui les constituent, ces lois aboutissent à des solutions différentes. Ce qui est sûr, c'est que toutes les solutions qui ont duré et passé le filtre de la sélection naturelle ont toujours été les plus économes en terme d’énergie à mettre en œuvre et de quantité de matière première à utiliser pour les former. Aussi, les phénomènes d'arborescence et de ramification (arbres, structure des cristaux de neige, fleuves au niveau d'un delta,...), les spirales (ADN, galaxies, coquilles d'escargot,...), les méandres et les tourbillons (turbulence, eau se

vidant d'un lavabo,...) sont nombreux dans le monde qui nous entoure car ce sont des formes d'organisation qui sont économes en terme d'énergie à mettre en œuvre pour les former. Newton a dit : "La nature ne fait rien en vain ; et le plus est vain si le moins suffit, car la nature aime la simplicité et ne s'embarrasse pas de causes superflues". Tout cela est bien abstrait me direz-vous : alors revenons à nos phénomènes de ramification et voyons un problème simple. Soit 4 points, disposés en carré, que vous voulez relier par la ligne la plus courte possible. A votre avis, quelle va être la forme de cette ligne? Posons le problème autrement : imaginez que vous devez construire un mur reliant les quatre coins d'un carré avec le plus petit nombre possible de briques. Quelle va être la forme de ce mur ? On remarque sur la figure suivante que différentes solutions sont possibles pour relier ces quatre points entre eux, mais la solution qui utilise la ligne la plus courte est celle du bas à droite. Vous aurez reconnu ici le motif de base d'un pavage hexagonal de l'espace.

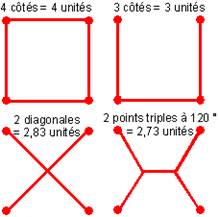
Ce simple exemple met en évidence un fait : l’utilisation de points triples est impérative pour minimiser les distances et est une constante dans les phénomènes d’arborescence et de ramification. Ne vous y trompez pas, ce ne sont pas des élucubrations de chercheurs un peu fous : ces notions sont utilisées par les entreprises de transport routier pour optimiser les trajets lors de livraisons sur plusieurs villes ou par les ingénieurs pour construire les structures des avions et des ouvrages d'art au moindre poids. En plus, si vous fabriquiez avec deux plaques et quatre plots, un petit montage tel que montré sur la figure ci-dessous et que vous le trempiez dans de l’eau savonneuse, vous vous rendriez compte que la bulle de savon qui se forme entre les quatre plots prendrait systématiquement cette forme là (figure ci-dessous).

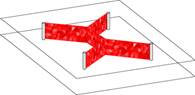
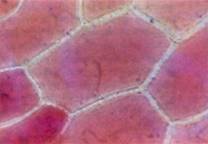
De nombreuses équipes de recherche dans le monde entier travaillent sur la compréhension des phénomènes liés à la physique des bulles de savon. L'enjeu est très important car il existe une analogie forte entre les bulles de savon et les membranes lipidiques qui séparent les cellules des êtres vivants. Comprendre les bulles de savon permet de mieux comprendre l’organisation des cellules entre elles, et donc la biologie des êtres vivants. Il suffit de regarder la photo suivante (cellules de l'épiderme d'un chou rouge) pour être convaincu que l'organisation des cellules entre elles suit les mêmes lois que celles qui régissent l'auto-organisation des bulles de savon ; il s'agit de la loi des surfaces minimales : la nature ne fait rien en vain...

Revenons à nos points triples. Si on y regarde de plus près, on découvre que l’utilisation de points triples est une constante dans la nature. Les abeilles n’ont pas appris les mathématiques, mais elles ont vite compris que pour paver l’espace en deux dimensions d’un cadre, c’est avec cette forme de base qu’elles construiront au moindre coût en cire et en efforts les alvéoles de leurs pouponnières.

Dans le monde minéral, lorsqu'une étendue d'eau s'assèche, la forme des fissurations ne contient presque que des points triples à 120° puisque c'est selon cette forme que les fissurations se produisent en dissipant un minimum d'énergie (bien sûr, des inhomogénéités locales modifient cette règle).

Les orgues de basalte produites lors des éruptions volcaniques s'expliquent par les mêmes lois. Cette notion de point triple qui minimise les critères de trajet minimum ou de surface minimum est à la base des phénomènes de ramification et les arbres fruitiers, comme tous les arbres, aussi ont "compris" que pour capter un maximum de soleil, et donc pour porter un maximum de feuilles, il fallait se ramifier. La ramification est un phénomène d'auto-organisation qui permet d'augmenter la surface extérieure de la plante, c'est-à-dire sa surface d'échange avec le milieu extérieur (pour pratiquer la photosynthèse), sans pour autant trop augmenter en volume. Les mêmes lois s'appliquent aux racines, la ramification utilisant des points triples est la solution la plus économe pour explorer un maximum d’espace à la recherche des nutriments nécessaires à la croissance de l’arbre. Aussi, au fur et à mesure que la plante poursuit sa croissance, la ramification aérienne et souterraine donne accès à l’espace tridimensionnel sans les inconvénients liés au volume. Tout l'art de la taille est d'ailleurs de faire un choix dans ces nombreuses ramifications de façon à imposer à l'arbre la forme que l'on désire pour favoriser le calibre et la qualité des fruits. Il est vrai que le but premier d'un arbre fruitier n'est pas de porter des fruits bien colorés et de gros calibre pour satisfaire l'arboriculteur qui l'a planté, mais de produire un maximum de pépins (ou de noyaux) pour garantir la survie de l'espèce, le fruit n'en étant que la protection extérieure.

Regardons maintenant d'un peu plus près la forme de la ramure et le port des arbres. Nous avions vu dans le précédent article que la fonction première de la couronne d'un arbre est d'offrir un maximum de surface foliaire aux rayons du soleil. On sait que l'angle moyen d'arrivée des rayons du soleil sur un arbre dépend de la latitude à laquelle il se trouve sur la Terre. Ainsi, les arbres ont-ils adopté une forme et un port adaptés à la latitude de la région où ils vivent. Partons de l'équateur où les rayons du soleil tombent à la verticale. Nul n'est alors besoin de garnir le côté de l'arbre de feuilles, elles ne serviraient à rien. La solution dans ces contrées est de mettre un maximum de feuilles sur le dessus de la couronne. La photographie ci-dessous montre un dragonnier dont la forme est typique des régions chaudes ou proches de l'équateur.

A l'autre extrême, dans les régions proche des pôles, on trouvera des arbres comme l'épinette du Canada qui auront tendance à monter très haut et à garnir leurs flancs d'un maximum de ramification pour capter la lumière d'un soleil souvent très bas sur l'horizon. Mécaniquement, cette forme est aussi bien adaptée aux chutes importantes de neige puisque les bras de levier sont très courts, contrairement à la forme du dragonnier dont les branches se déchireraient au niveau des fourches, si elles étaient soumises à un poids important.

Dans nos régions tempérées, la forme naturelle des arbres est un compromis entre ces deux types de port (voir plus bas, la photo d'un Boskoop) et une forme se rapprochant plus d'une boule est très souvent utilisée par les arbres pour capter un maximum d'énergie lumineuse. Nous venons donc de voir ici trois façons différentes de ramifier que l'on peut facilement exprimer en équation dans un modèle pour simuler ces formes d'arbre.

Après avoir vu la nécessité de la ramification pour une exploration optimale de l'espace, continuons maintenant à la manière des mathématiciens à complexifier notre modèle. Comment bien rendre compte des angles et des diamètres des branches à chaque ramification calculée? Et bien, les diamètres des branches et l'angle qu'elles font entre elles sont liés par des lois! On a vu que le rôle de la ramure d'un arbre est avant tout de porter des feuilles. Cette ramure doit aussi leur assurer le transport des nutriments par la circulation de la sève brute et de la sève élaborée. Cette fonction va avoir une influence considérable sur la manière de ramifier. La théorie qui décrit ce que l'on peut appeler les arborescences d'écoulement (par opposition aux arborescences de support) est régit par la "loi de Murray". Voyez ces deux photos : à gauche un Boskoop, à droite une artériographie d'un rein humain. Pour une même fonction, distribuer un liquide dans l'ensemble d'un volume restreint, la nature applique une même solution : la ramification!

Que le fluide qui circule dans les deux arborescences soit de la sève ou du sang, la loi de Murray permet de modéliser les phénomènes de circulation de tout fluide dans une structure ramifiée. En particulier, cette loi montre (schéma de gauche) que le rapport des diamètres entre une conduite secondaire de diamètre D2 et la conduite principale de diamètre D1 est lié à l'angle A que font les deux branches entre elles. Tous les arboriculteurs pratiquant la taille utilisent cette loi et savent que l'angle que fait une branche par rapport à la conduite principale déterminera le diamètre de cette branche : si on veut freiner sa croissance, on va la mettre plus à l'horizontale, si on veut la privilégier, on la ramènera à la verticale.

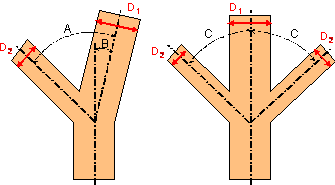
On peut donc dire que lorsque l'angle tendra vers 90°, c'est-à-dire vers l'horizontale pour la branche secondaire, alors D2 / D1 deviendra très petit. Par contre, avec un angle très fermé, on aura deux branches sensiblement de même diamètre et D2 / D1 sera proche de 1. Ce phénomène peut très bien se voir un an après le rabattement d'un scion au moment de la plantation. Ce sont bien les rameaux qui partent avec un angle proche de 90° qui ont les diamètres les plus petits et que le novice aura tendance à couper pour garder les plus gros, proches du point de rabattement, qui sont généralement les concurrents à la flèche puisqu'ils ont poussé avec un angle très (trop) fermé par rapport à la verticale.

Vérifions la loi de Murray pour les arbres que nous venons de voir en photo :

La loi de Murray décrit un deuxième phénomène intéressant : lorsqu'une branche secondaire se développe, la branche principale va légèrement s'infléchir dans la direction opposée selon un angle B par rapport à la verticale (partie gauche du schéma plus haut) et plus le diamètre de la branche secondaire sera grand, plus cette inflexion sera importante. Cette réaction permet à l'arbre, au fur et à mesure de sa croissance, de conserver son centre de gravité à la verticale de son point de fixation au sol (racine).
Dernier point : si deux branches secondaires partent de manière opposée de la branche principale (partie droite du schéma plus haut), la conduite principale ne sera pas déviée, mais on gardera pour les deux branches secondaires les mêmes propriétés que celles expliquées pour une seule branche secondaire. A vos mètres rubans et rapporteurs et partez dans la nature prendre des mesures ! Vous établirez ainsi vous-même les diagrammes de Murray en reportant les points mesurés dans un diagramme comportant, en abscisse, le rapport des diamètres branche secondaire / branche principale (variant de 0 à 1) et, en ordonnée, l'angle que font les branches entre elles (variant de 0° à 90°). La courbe en rouge, figure ci-dessous, est la courbe D2 / D1 en fonction de A.

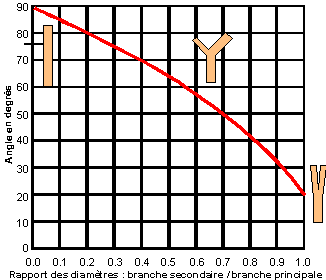
Naturellement, il s'agit là d'une courbe de tendance qui varie en fonction des espèces, et dans une même espèce, en fonction des variétés. Si vous essayer de tracer cette courbe vous-même, veillez bien à toujours prendre des fourches où les deux branches ont sensiblement le même âge. Bien évidemment, cette loi ne sera pas valable pour un rameau provenant d'un œil latent sur un tronc vieux de dix ans, par exemple après une taille trop sévère !
Pour l'instant, en observant les diamètres et les angles, nous nous sommes contentés de constater un fait. Mais pour quelle raison les choses sont-elles ainsi ? La loi de Murray est en fait la conséquence de la minimisation de l'effort à fournir dans le transport de la sève d'un point à l'autre: il s'agit là d'un problème d'hydrodynamique. Une fois encore, la nature ne fait rien en vain... Il est facile de comprendre que la sève circule en dissipant moins d'énergie dans un gros tuyau que dans un petit. Plus le diamètre du tuyau sera petit et plus les frottements dus à la paroi très proche vont être importants. Comme on le voit sur le schéma ci-dessous, pour relier une feuille dans la couronne à une grosse branche, on a deux possibilités à partir d'un point triple
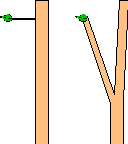.Soit la sève va parcourir un maximum de distance dans une canalisation de fort diamètre, (la branche principale) jusqu'à arriver à proximité du point en question, et un minimum de distance dans la canalisation de faible diamètre qui relie le point en question à la branche principale (cas de gauche). Cette condition est satisfaite si la branche secondaire part de la branche principale avec un angle très ouvert. Ou bien, pour rallier ce point, la bifurcation va se faire avec un angle très fermé (cas de droite). Vu qu'il reste une grande distance à parcourir le diamètre de la branche en question doit alors impérativement augmenter. Suivant les circonstances, la nature choisi l'une ou l'autre des solutions. Sachez que les diagrammes de Murray ont d'abord été établis pour les arborescences d'écoulement dans le corps humain (circulation sanguine) et utilisés plus tard en biologie végétale. La publication originale de Cecil D. Murray date de 1926 et est téléchargeable sur le site du Journal of General Physiology en tapant  http://www.jgp.org/cgi/reprint/9/6/835.pdf . Murray c'était d'ailleurs inspiré des travaux d'un certain Wilhelm Roux datant de 1878. Les courbes représentant les angles en fonction des rapports de diamètres n'ont d'ailleurs pas la même allure dans les deux cas car, contrairement aux réseaux de veines dans un organe, un arbre pousse en s'opposant à la pesanteur. Il doit donc, lorsque deux grosses branches se séparent, produire des angles plus fermés que ne le produisent les veines lorsque qu'elles se séparent, pour des questions de solidité mécanique. On le voit nettement sur la photo de l'artériographie du rein : dans le corps humain de grosses veines peuvent se séparer de l'artère principale avec des angles très grands proches de 90°, ce que les arbres font rarement à cause de la pesanteur. En fait, pour les réseaux ramifiés d'artères et de veines, la pesanteur est secondaire par rapport à la lutte pour l'espace disponible.
J'espère à travers cette approche simple et ludique, mais de loin non exhaustive, des mathématiques appliquées à l'arboriculture et à la biologie en général, vous avoir donné envie d'en savoir plus sur les phénomènes d'auto-organisation dans la nature. Pour ceux qui veulent approfondir ce sujet, voici LE site de référence sur lequel je me suis appuyé pour la rédaction de cet article : le cours en ligne de Jean de Vaugelas, professeur à l'Université de Nice, Sophia Antipolis sur le thème "Biodiversité, Contraintes et Evolution" sous l'adresse http://www.unice.fr/LEML/coursJDV/
index2.html . Les études dans ce domaine de recherche sont relativement récentes, couvrent un grand nombre de disciplines et beaucoup reste encore à découvrir (un  texte sous http://csiweb2.cite-sciences.fr/derosnay/articles/chap1.htm fait le tour de la question).

En biologie, les mécanismes d'auto-organisation semblent être impliqués dans l'homéostasie, l'établissement de la polarisation cellulaire, les réseaux métaboliques, la différenciation cellulaire et le développement... Des modèles d'auto-organisation sont aussi utilisés pour prévoir les mouvements de foule, l'évolution des grandes métropoles, l'adaptation des écosystèmes et le comportement des insectes vivants en sociétés (abeilles, termites, fourmis,...) Il s'agit de phénomènes essentiellement collectifs où les propriétés d'un ensemble ne peuvent pas se réduire à la somme des propriétés des éléments qui le composent. D'un désordre local émerge une structure organisée : on rejoint là, les notions d'émergence et d'apparition de la vie sur terre.

L'étude des phénomènes d'auto-organisation montre qu'à toutes les échelles de grandeur, de l'infiniment petit à l'infiniment grand, la symétrie et la beauté font partie intrinsèque de la nature. Les contraintes imposées par les lois physiques n'empêchent pas une très grande variété de formes finales : la diversité des espèces en est un exemple. C'est l'exploration au cours du temps de toutes les nuances autour de thèmes majeurs, comme la ramification, qui est le secret de la biodiversité passée, présente et, on l'espère, future.

Frank Christnacher

Article paru dans la revue Fruits et Abeilles.

HOME ACCUEIL  les crets fruits et pomologie